
 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005.
Tous droits réservés pour tous pays. All rights reserved. |
Prediction of the Spatial Informations for the Control of Room Acoustics Auralization
Federico Cruz-Barney et Olivier Warusfel
AES: Convention of the Audio Engineering Society, New York City, Etats Unis, Septembre 1997
Copyright © Audio Engineering Society 1997
Abstract
This paper presents some results on a study aiming at accessing the spatial information needed for the recreation
of realistic binaural impressions of enclosed spaces from
echograms simulated by a room acoustics predictive software
developed at IRCAM. After a brief description of the
software and of the general principle of auralization in
computer models, a simple formulation to obtain the binaural
criteria IACC using the predictive software is explained and
some attempts to validate it are made.
Introduction
In order to recreate realistic auralizations of the acoustics of enclosed
spaces, one usually convolves an anechoic signal (music, speech,...) with
binaural impulses obtained either from measurements with a dummy head in a
real room or a scaled model, or by simulations with a computer model. When the
simulated outputs of a predictive software are instead given in the form of
energy-time curves (ETC), as with the present software, convolution is no
longer possible and the necessary spatial informations for the binaural
reproduction of the entire soundfield is not directly accessible. This paper
presents a method aiming at compensating for the lack of spatial information
of the ETC by the estimation of an associated mean incidence vector per
temporal segment at each one of the receiving positions. The calculated mean
incidence vectors are then used to control the spatial cues of the different
time sections.
As an example, a simple method to calculate the interaural
cross-correlation coefficient IACC from our computer software using this
principle is proposed in order to have access to binaural auralizations.
After a brief description of the main characteristics of the predictive
software developed at IRCAM, the basic principle of the auralization process
that we use is explained, followed by an explanation of the method
proposed. Finally, an attempt to validate it is done using a data base
gathered from a measurement campaign undertaken at IRCAM's Espace de
Projection.
Description of the room acoustics predictive software
The room acoustics laboratory at IRCAM has developed a room acoustics
predictive software [1] that combines various physical models of
sound propagation to estimate the energy-time curves at different receiver
locations. These models include plane wave propagation with specular
reflections, diffraction and diffuse reflections. The combination of these
methods is derived from preliminary studies showing their complementarity when
estimating different criteria linked to the acoustical quality of a
hall. Figure 1 shows a schematic description of the models involved in the
prediction process, briefly explained in the following paragraphs.
- Diffraction model (step 1). In the presence of an orchestra pit or loggia
in an Opera house, a geometrical masking of the direct sound will occur for
certain parts of the audience. In such a case, the diffusion and the specular
reflection model would reflect the energy back into the incident half space,
considering that complete masking occurs, instead of a resulting diffracted
wave. The perceptual importance of the direct sound has led to the
introduction of a diffraction model to account for this sort of situation.
- Model of plane wave propagation and specular reflections (step
1). The plane wave propagation is simulated by an algorithm combining an image
source model up to second order reflections with a cone method
for the prediction of higher orders of reflections.
- Diffuse propagation model (step 2). In order to take into
account the non-specular character of reflections, the preceeding models are
coupled to a method based on the hypothesis of ideally diffuse reflections
(Lambert's law). The combination of the specular and the diffuse models is
managed for every reflection according to a diffusion coefficient depending on
the nature of the walls (or facets). The fraction of energy not specularly
reflected nor absorbed is propagated between the room boundaries according to
a transfer matrix, computed during a preliminary process (step 0 in figure 1),
and that describes the time and space discretisation of Kuttruff's integral
equation [2].
- Late energy propagation (step 3). After a transition time (Tt), the cone
method and the direct diffusion processes are stopped and the residual
energies present on the boundaries are used for the calculation of the late
energy distribution. Assuming an exponential decay, the amplification of this
residue is calculated for each boundary and the corresponding energy
contributions are checked on each receiver location (figure 2). Hence the late
energy distribution will depend on the following parameters:
- distribution of the residual intensity when the cone tracing method is stopped;
- amplification of this residue during the exponential decay;
- geometrical coupling of the receivers with each surface.
This particular method gives access to the distribution of the late reverberant
field, which under some circumstances may not be homogeneous, as is the case
with balcony overhangs.
The reverberation time may be obtained from procedures described in
[1][3].
The usual energy-based parameters which characterize the acoustical quality
are then derived by subdividing the energy-time curves into temporal segments
or ``pre-criteria'' (see table 1).
Auralization in computer models
When dealing with the computer modelling of binaural impulse responses (BIR),
the early and late parts are often obtained by separate procedures
[4][5]. The early part is generally calculated by inverse
Fourier transform of the transfer functions of the minimum-phase equivalent
filters characterising the different phenomena encountered by each sound ray
along its propagation path for a given source/receiver couple. They include
the source directivity, the air absorption, wall reflections and diffraction
from the listeners head, torso and ears (as measured by the Head related
Transfer Functions, HRFT). The later part of the BIRs can be synthesised
using various statistical approaches. One of them consists in substituting the
late part of the response with white noise filtered according
to the mean absorption of room boundaries, to the air absorption and to the
diffused field response of the source and the receiver
[5]. Another approach consists in creating the late
part by a simplified process associated to a shoebox shaped hall with the same
mean free path, absorption factor and surface area as the actual hall
[4]. A simulation of the auralization inside the model is then
obtained by convolution of the entire binaural response with an anechoic
signal. Its performances when compared to the simulated space will depend on
the different physical models used to characterize the sound propagation,
transducers characteristics, halls geometry and the materials data
base. However, the results obtained are only valid for a single
source/receiver couple and so the BIRs have to be recalculated for every
source or receiver position and orientation. Another inconvenience comes from the fact that
the procedure is based on a binaural encoding of spatial cues, thus
auralizations will only be valid for an individual reproduction on headphones
(binaural mode) or two loudspeakers via a cross-talk cancellation filtering
matrix (transaural mode). This
limitation can be partially overcome when encoding the acoustic field at a
receiving position with the 4-channel Ambisonic ``B format'', which is
equivalent to the coincident association of an omnidirectional microphone and
three orthogonal bidirectional microphones [6]. In this case,
Ambisonic decoders can accommodate various multichannel loudspeaker layouts of
typically four to eight loudspeakers and allow a post processing to simulate
orientation effects of the receiver [7].
An alternative approach for the auralization consists in describing the
acoustical quality perceived at each receiver location by a set of parameters
instead of an impulse response, and to synthesize the room effect according to
these parameters. In the present case this synthesis is performed by the
Spatialisateur, a virtual acoustics processing software developed at
IRCAM and Espaces Nouveaux [8]. The Spatialisateur
synthesizes, in real time, a generic room effect which is controlled
by a set of parameters issued from research carried out at ENST and IRCAM
[8][9]. This generic room effect is based on a simplified
temporal distribution of the energy, consisting in four time sections (figure 3). After synthesis of the time distribution, the Spatialisateur
controls the spatial informations associated to the different time sections:
localisation control for the direct sound and early reflections (OD + R1), and
control of the IACC for the binaural reproduction of the cluster
and the late reverberation (R2 + R3).
The energy of the time sections may be computed from the ETCs generated by the
room acoustics predictive software. On the contrary, the spatial informations
associated to each section are not directly accessible. Hence, the control of
the spatial parameters of the Spatialisateur requires some additional
information given by the computer model and described below.
- Direct sound. The spatial information related to the direct sound
is of special importance since it will govern the localisation of the
source. However, in case of direct sound masking, linked to diffraction by room edges
or to directivity characteristics of the source, this first contribution might
be substituted with the first reflection. The spatial information provided to
the Spatialisateur is simply the direction of incidence of the sound path
associated to this first contribution. The Spatialisateur will use this
directional information to synthesise the localisation according to the chosen
reproduction setup.
- Early reflections. Concerning the early reflections, a direction
of incidence can be associated to each one of the reflections synthesised by
the Spatialisateur, as for the direct contribution. However, some
studies [10] suggest that auditory perception may not be sensible
to the fine structure of the early reflections distribution. Hence, it may be
envisionned to simplify the spatial description of this time section, which can
lead to save signal processing cost, especially when using binaural
coding. A simplification is proposed in [11]. It consists in
keeping the interaural gain and delay differences for each reflection
and to filter the whole early reflections section by the use of a common
filter. This common filter can be calculated from the HRTFs associated
with the reflections included in that time section and weighted
by their respective energies.
- late reverberation. In order to characterize the perceived spatial
effect associated to the late reverberant energy, the computer model should
provide an estimation of the interaural cross-correlation coefficient IACC
[12][13][14].
One of the advantages of this parametrical approach is to provide a description
of the auditory scene independently from the reproduction configuration. Whereas
a characterization based on impulse responses will be more constraining, for it
is linked to a specific encoding format of the spatial information. More
generally, such a parametrical approach allows post-processing operations.
For example, the head-tracking, used to compensate for the movements of the
listener during the auralization, may be easily implemented since it consists in
a correction of the directionnal parameter send to the Spatialisateur.
Hence it does not involve additional processing cost.
Estimation of the spatial cues
In order to estimate the spatial cues associated to the time sections of the
ETC, the description of the spatial distribution of reflections is synthesised
in the form of simple indices. For this purpose, a mean incidence vector 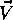 is
calculated. The norm of this vector will provide the information about
the diffuseness of the soundfield at a particular time section and its
orientation will translate a lateralization effect eventually perceived by a
listener. These informations will be used to estimate an IACC associated to
a particular time segment.
is
calculated. The norm of this vector will provide the information about
the diffuseness of the soundfield at a particular time section and its
orientation will translate a lateralization effect eventually perceived by a
listener. These informations will be used to estimate an IACC associated to
a particular time segment.
In the following paragraphs the calculation of the mean incidence vector
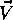 is explained along with the description of a method proposed by
Nakajima et al.[15] for the estimation of the IACC and
an alternative simple method which relates
is explained along with the description of a method proposed by
Nakajima et al.[15] for the estimation of the IACC and
an alternative simple method which relates 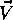 with possible IACC values for given temporal sections of the ETC.
with possible IACC values for given temporal sections of the ETC.
Calculation of the mean incidence vector V
For every one of the energy contributions (specular or diffused) to a specific receiver, the mean
incidence is calculated and weighted according to the amount of energy carried
by the contribution as well as to the receivers directivity. A vector
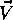 of components (
of components ( 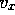 ,
, 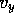 ,
, 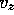 ) as viewed from each
receivers coordinate system is then constructed, where
) as viewed from each
receivers coordinate system is then constructed, where 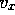 corresponds to
the receiver pointing direction,
corresponds to
the receiver pointing direction, 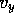 to the lateral direction and
to the lateral direction and 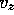 to the upward/downward direction. Once this vector is known, its three
components will provide the vertical and horizontal (
to the upward/downward direction. Once this vector is known, its three
components will provide the vertical and horizontal (  ,
,  ) angles of
incidence for a particular time section. The IACC can be estimated from
the vectors norm
) angles of
incidence for a particular time section. The IACC can be estimated from
the vectors norm 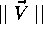 and from an equivalent angle
measured from the receivers median plane, a lateralization angle
and from an equivalent angle
measured from the receivers median plane, a lateralization angle
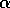 of the soundfield as seen from the receiver, where
of the soundfield as seen from the receiver, where
 . This approximation is
justified since we can consider the head as being almost symmetrical, so the
IACC is mainly determined from the reflection angle measured from the
median plane [15].
. This approximation is
justified since we can consider the head as being almost symmetrical, so the
IACC is mainly determined from the reflection angle measured from the
median plane [15].
Nakajima's method for the estimation of IACC
For the estimation of the IACC within the context of computer
simulations, a proposed procedure is inspired from a method developed by
Nakajima et al.[15], where a simple equation to calculate
the IACC was derived. The method consists on the recreation of the
interaural cross-correlation function CCF by the superposition of the
elementary CCF cumulated for each reflection and for a specific frequency
band. The normalized value of the resulting CCF for N discrete and
incoherent reflections at both ears of a human or dummy head can be expressed
in the following terms:
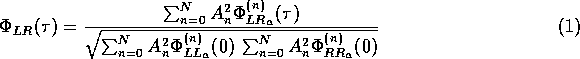
where  is the time delay of sound signals between both ears, and ranges
from -1ms to +1ms to include the maximum interaural delay.
is the time delay of sound signals between both ears, and ranges
from -1ms to +1ms to include the maximum interaural delay. 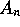 is the
pressure amplitude of the nth reflection relative to the direct
sound.
is the
pressure amplitude of the nth reflection relative to the direct
sound. 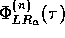 is the CCF of the signals for the
nth reflection and its associated lateralization angle
is the CCF of the signals for the
nth reflection and its associated lateralization angle 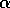 .
.
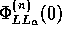 and
and  are
autocorrelation values ACF at
are
autocorrelation values ACF at  =0 (arrival time of the direct sound) of the
signals at the left and right ears, for the nth reflection and
associated lateralization angle
=0 (arrival time of the direct sound) of the
signals at the left and right ears, for the nth reflection and
associated lateralization angle 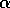 .
The interaural cross-correlation coefficient IACC corresponds to the maximum
absolute value of the function.
.
The interaural cross-correlation coefficient IACC corresponds to the maximum
absolute value of the function.
The independent bandpass-filtered components of the CCF of centre frequency
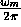 , are calculated by the following equation:
, are calculated by the following equation:
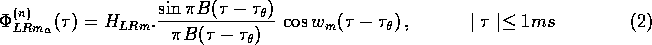
where 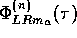 is the CCF per octave band ( m ) of
the signals for the nth reflection, B is the effective bandwidth of the
noise;
is the CCF per octave band ( m ) of
the signals for the nth reflection, B is the effective bandwidth of the
noise; 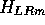 is the crosspower of mth bandpass filtered source signals
at both ears normalized by that of
is the crosspower of mth bandpass filtered source signals
at both ears normalized by that of 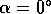 (frontal incidence).
The value of
(frontal incidence).
The value of 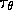 indicates the delay at the maximum of the
cross-correlation function, which depends on
indicates the delay at the maximum of the
cross-correlation function, which depends on 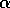 .
.
Estimation of IACC from the mean incidence vector V
Since for a given sound signal, the IACC will be a function of the directions
as well as of the amplitudes of sound reflections arriving at a receiver, an
approximated method is now proposed to relate the vectors 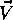 to possible
IACC values.
to possible
IACC values.
The maximum possible IACC value per octave band for a given
angle of incidence is obtained in free field. For that particular case, the
norm of the mean incident vector 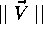 will equal unity. In an
ideally diffuse sound field, the cross-correlation between two omnidirectional
microphones is related to the ratio sin(kr)/kr, r being the distance
between both receivers. At low frequencies, the receivers will be closer to
each other relative to the wavelength, so high correlations are to be
expected. While
will equal unity. In an
ideally diffuse sound field, the cross-correlation between two omnidirectional
microphones is related to the ratio sin(kr)/kr, r being the distance
between both receivers. At low frequencies, the receivers will be closer to
each other relative to the wavelength, so high correlations are to be
expected. While 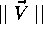 will reach a value very close to zero at
all frequencies, IACC will vary depending on the octave band.
will reach a value very close to zero at
all frequencies, IACC will vary depending on the octave band.
The mean incidence vectors obtained in the precedent section for given
temporal segments and for specific frequency bands are then related with a
simple equation to possible IACC values ranging from supposed minimum
diffuse field IACC( )D up to a maximum established by a set of
free field measurements which will depend on the lateralization angle
)D up to a maximum established by a set of
free field measurements which will depend on the lateralization angle
 . So, each estimated IACC(
. So, each estimated IACC( ) per time segment from
simulations, IACC(
) per time segment from
simulations, IACC( ,t) will be a function of the following variables:
the free field IACC(
,t) will be a function of the following variables:
the free field IACC( ,
, ), the diffuse field
IACC(
), the diffuse field
IACC( )D and
)D and 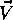 :
:
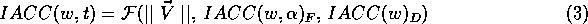
Validation of the method from a measurements data base
A measurement campaign has been undertaken at IRCAM's Espace de
projection, a variable acoustics rectangular room by means of an adaptable volume
( 1800m3 - 3800m3) and rotating panels covering all walls and ceiling
[1]. The data base gathered from this campaign has been used to
validate the method for the estimation of the IACC using the room acoustics
predictive software developed at IRCAM. In this section, the measurement
campaign is explained and the results obtained are shown along with the
validation procedure.
Measurement campaign
The impulse response measurements were carried out using an MLS based
measurement system. A dodecahedron loudspeaker was used as the sound source which
was placed on the axis of the room at some distance to the back wall. Two Shoeps
electrostatic microphones of the colette series, with a multidirectional
capsule model MK6 in its omnidirectional configuration and attached to a home
made dummy head were used as receivers (figure 4). Four receiving positions
and four room configurations with a fixed volume were tested, giving a total of sixteen
source/receiver combinations. The room configurations were the following:
- AA: All of the acoustic panels of the room (ceiling + walls) in
the absorbent position.
- RR: All of the acoustic panels of the room (ceiling + walls) in
the reflecting position.
- AR: All of the front half of the room (ceiling + walls)
absorbent, the back half reflecting.
- RA: All of the front half of the room (ceiling + walls)
reflecting, the back half absorbent.
IACC values for the 3 octave bands centred at 250Hz, 1KHz and 4KHz were derived
from the impulse responses measured at both ears of the dummy head selecting
the maximum absolute value of the interaural cross-correlation function (CCFt( ))
within the integration limits t1 and t2:
))
within the integration limits t1 and t2:
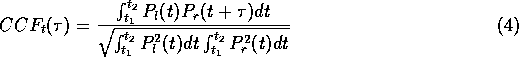
where l and r represent the left and right ears respectively, and  the time shift, ranging from +1ms to -1ms to include the maximum
interaural delay.
the time shift, ranging from +1ms to -1ms to include the maximum
interaural delay.
For the validation of the method, simulations on the computer model of the
Espace de projection were performed for all the acoustical configurations and
according to the same spatial disposition, directivity and orientation of the
transducers.
Comparisons between the estimated and measured IACC for the time range from [0 - 80ms], IACC80 and the three octave bands are presented and discussed in the next paragraphs.
Results and discussion
As a first approach to the validation procedure, some preliminary results from
comparisons at the 250Hz, 1KHz and 4KHz octave bands between measured and
estimated IACC80 are presented.
In order to have an idea on the objective differences between the
configurations tested, table 2 shows the measured and simulated reverberation
time (RT) variability. The measured (RTs presented are the mean values of the
left and right ears at all of the receiving positions for a given
configuration. Eventhough the RT change from the most absorbent to the most
reflective configuration is quite important, as seen in table 2, the IACC80
range between configurations is relatively small, for the geometry of the room
remained unchanged during the measurement campaign. As a result, the
robustness of the validation is somehow limited.
Table 3 illustrates the overall statistics of the measurement
campaign. From the mean difference between measurements and the computation model
we see that there is a tendency to
underestimate IACC80 for all three frequency bands, a
tendency very much accentuated at receiver position R2, which is probably
related to a particular reflection pattern associated to this receiver
position.
Although the Standard Deviation (STD) statistics show that estimated values variate
less than the measured ones, the inter-receiver and inter-room
configuration variations are well predicted, as seen from the Mean Absolute
Error results (after correction of the global difference), and from the Correlation
Coefficients. Figure 5 shows inter-receiver variation results for the
three frequency bands tested and for room configuration RR. An example of
inter-room configurations estimation is presented in figure 6. Results for
configurations AR and RA and for two receivers, R2 facing the first half of the
room and close to the source, and R4, far from the source and in the back half
of the room (see figure 4) are given. For room configuration RA, low correlation
values are expected for receiver R2, since for the time segment studied strong
reflections will hit the receiver from a relatively wide solid angle, whereas
for R4, reflections coming from a smaller solid angle will predominate,
because it is surrounded by absorptive surfaces. In this case then,
higher IACC80 are expected. The estimated IACC80 follow this
trend quite well, as for the opposite situation (configuration AR) where
correlation values at receiver R2 will be higher than for the precedent
configuration and will diminish at receiver R4.
The observed differences found concerning the smaller estimated variations in
relation to the measured ones and the global underestimated IACC80 ,
may be related to the approximations inherent to the estimation method in the
one hand, and to the fact that, because the 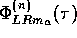 are periodical functions with several maxima (their separation depending on
frequency), reflections coming from different directions interfere with each
other and contribute to increase the measured inter-receiver variability, on
the other. Actually our method is closer to an approximation of the CCF by
their envelopes, i.e. where the estimation of the IACC from the mean
incident vector is equivalent to the estimation of IACC calculated from the superposition
of the envelopes of the
are periodical functions with several maxima (their separation depending on
frequency), reflections coming from different directions interfere with each
other and contribute to increase the measured inter-receiver variability, on
the other. Actually our method is closer to an approximation of the CCF by
their envelopes, i.e. where the estimation of the IACC from the mean
incident vector is equivalent to the estimation of IACC calculated from the superposition
of the envelopes of the 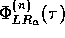 in equation 1.
in equation 1.
Conclusions
A simple method for the calculation of the spatial cues associated to the
different time sections of the simulated ETCs from our room acoustics
predictive software has been presented. This method includes the estimation of
the IACC in order to have access to binaural auralizations. For the
validation of the method, IACC estimations in three frequency bands have
been compared to a data base gathered from a measurement campaign undertaken
at IRCAM's Espace de projection.
For the measurement sample tested, results are coherent. Both inter-receiver
and inter-room configuration variations are well predicted. The
global differences found concerning the estimated variability, as given by the
STD, and the error estimation related to the measured IACC80 are
probably the consequence of the method approximations that do not consider
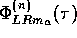 periodicity.
periodicity.
To further validate the method and confirm this behaviour, the measurements
data base has to be extended to other room shapes and sizes. Time intervals
without the direct sound must be compared since the examples tested were
very much influenced by the direct sound because of the receivers proximity
to the sound source.
References
- 1
-
Christian Malcurt.
Simulations informatiques pour predire les critères de
qualification acoustique des salles. Comparaison des valeurs mesurées et
calculées dans une salle à acoustique variable.
PhD thesis, Université de Toulouse, 1986.
- 2
-
Heinrich Kuttruff.
Room Acoustics.
Elsevier Applied Science, London, 3rd edition, 1991.
- 3
-
E.N. Gilbert.
An iterative calculation of auditorium reverberation.
J. Acoust. Soc. Am., 69(1):178-184, 1981.
- 4
-
Bengt-Inge Dalenback.
Room acoustic prediction and auralization based on an extended
image source model.
PhD thesis, Chalmers University of Technology, Göteborg,
Sweden, 1992.
- 5
-
Marc Emerit.
Simulation binaurale de l'acoustique de salles de concert.
PhD thesis, Institut National Polytechnique de Grenoble, 1995.
- 6
-
M.A. Gerzon.
Ambisonics in multichannel broadcasting and video.
J. Audio Eng. Soc., 33(11), 1985.
- 7
-
Jean Marc Jot.
Real-time spatial processing of sounds for music, multimedia and
interactive human-computer interfaces.
Multimedia Systems Journal. Special issue on Audio and
Multimedia, 1997.
- 8
-
Jean Marc Jot.
Etude et réalisation d'un spatialisateur de sons par modèles
physique et pérceptifs.
PhD thesis, Ecole Nationale Supérieure des Télécommunications,
1992.
- 9
-
Jean-Pascal Jullien.
Structured model for the representation and the control of room
acoustical quality.
In 15th Intl. Congress on Acoustics, Trondheim, Norway, pages
517-520, 1995.
- 10
-
D.R. Begault.
Binaural auralization and perceptual veridicality.
In Proc. 93rd Audio Eng. Soc. Convention, San Francisco, USA,
preprint 3421 (M-3), 1992.
- 11
-
Jean Marc Jot, Olivier Warusfel, Eckhard Kahle and Mireille Mein.
Binaural concert hall simulation in real time.
In IEEE Mohonk workshop, Oct 17-20, 1993.
- 12
-
J.S. Bradley.
Comparison of concert hall measurements of spatial impression.
J. Acoust. Soc. Am., 96(6):3525-3535, 1994.
- 13
-
P. Damaske and Y. Ando.
Interaural Crosscorrelation for Multichannel Loudspeaker
Reproduction.
Acustica, 27(1):232-238, 1972.
- 14
-
Takayuki Hidaka, Leo L. Beranek and Toshiyuki Okano.
Interaural cross-correlation, lateral fraction, and low- and
high-frequency sound levels as measures of acoustical quality in concert
halls.
J. Acoust. Soc. Am., 98(2):988-1007, 1995.
- 15
-
Tatsumi Nakajima, Jun Yoshida and Yoichi Ando.
A simple method of calculating the interaural cross-correlation
function for a sound field.
J. Acoust. Soc. Am., 93(2):885-891, 1993.
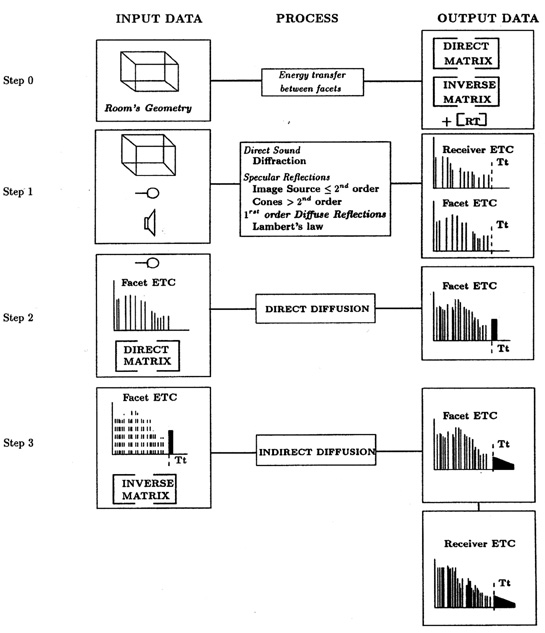
Figure 1: Schematic description of the room acoustics software. Tt stands for transition time
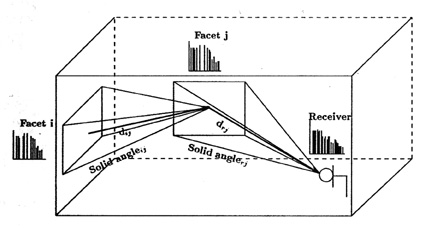
Figure 2: Diffuse energy transfer between facets and imputation to receivers
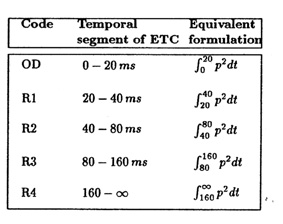
Table 1: Temporal segmentation of the energy-time curve (ETC) for the
calculation of energy-based criteria. The integrals temporal limits are given
in ms. The zero corresponds to the arrival time of the direct sound signal
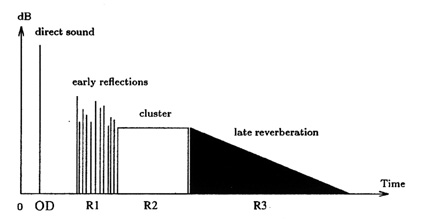
Figure 3: Generic room effect created by the Spatialisateur. Typical temporal segmentation of it is as follows: OD=[0,20]ms, R1=[20,40]ms, R2=[40, 100]ms, R3=[100,  ]ms
]ms
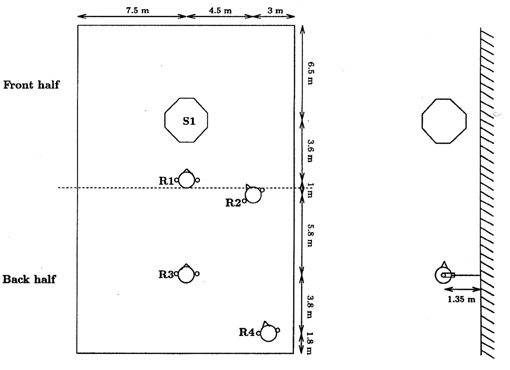
Figure 4: Configuration setup for the measurement campaign at the Espace de projection. Source (S1) and receivers (R1 - R4) placement. The ears
of the dummy head correspond to the omnidirectional microphones
| Centre Frequency |
Configuration |
Measured RT |
Simulated RT |
|
| 250Hz |
AA |
0.923 |
1.011 |
|
RR |
2.371 |
2.433 |
|
AR |
1.361 |
1.480 |
|
RA |
1.492 |
1.606 |
| 1KHz |
|
AA |
1.258 |
1.207 |
|
RR |
3.018 |
3.058 |
|
AR |
1.813 |
1.922 |
|
RA |
1.821 |
1.922 |
| 4KHz |
|
AA |
0.965 |
0.942 |
|
RR |
2.138 |
2.239 |
|
AR |
1.401 |
1.382 |
|
RA |
1.401 |
1.474 |
|
Table 2: Reverberation times measured (in seconds) and simulated at the
Espace de Projection. The measured RT are the mean of the four positions for the left and right ears.
| Centre Frequency |
Measured Iacc STD |
Estimated Iacc STD |
Average difference between Sim and Meas |
Mean Absolute Error (after correction of global difference) |
Correlation Coefficient |
|
| 250Hz |
0.162 |
0.157 |
-0.005 |
0.027 |
0.854 |
| 1KHz |
0.225 |
0.188 |
-0.064 |
0.051 |
0.801 |
| 4KHz |
0.206 |
0.191 |
-0.053 |
0.030 |
0.967 |
|
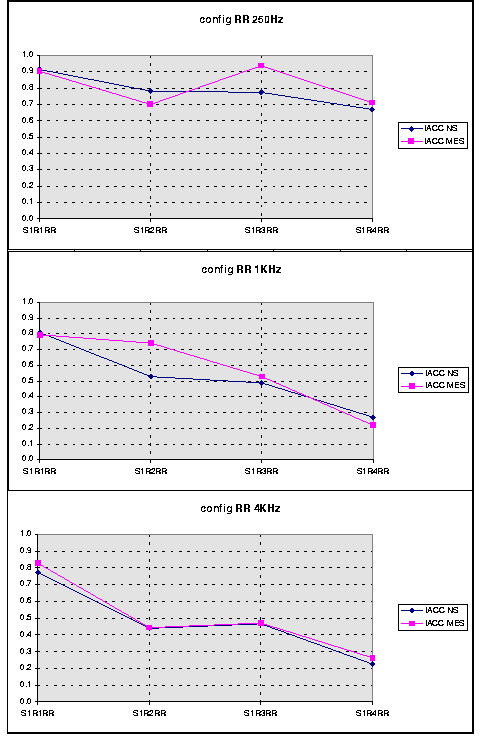
Figure 5:Comparison between measured and estimated IACC80 for a single configuration, on source (S1) and four receiver positions (R1 - R4)
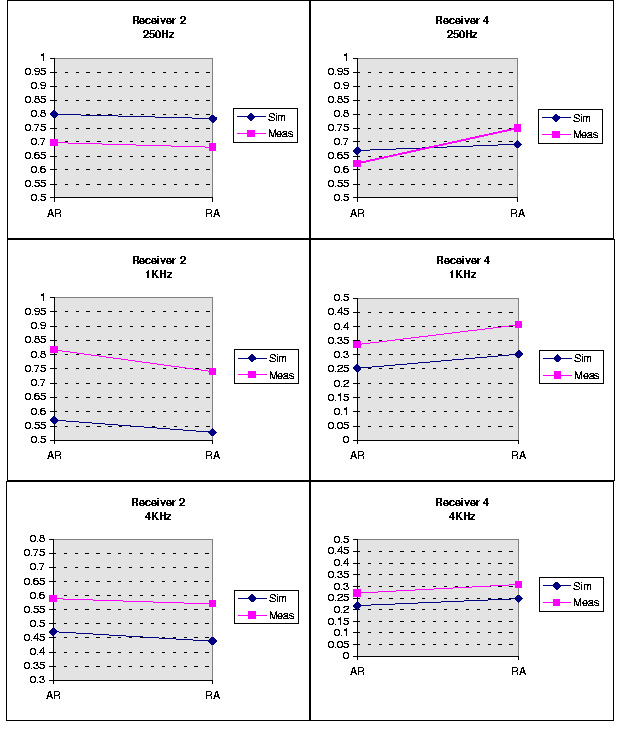
Figure 6:Comparison between measured and estimated IACC80 for two receivers (R2 and R4 ), one source (S1) and two rooms configurations variability
____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .
____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .



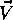 is
calculated. The norm of this vector will provide the information about
the diffuseness of the soundfield at a particular time section and its
orientation will translate a lateralization effect eventually perceived by a
listener. These informations will be used to estimate an IACC associated to
a particular time segment.
is
calculated. The norm of this vector will provide the information about
the diffuseness of the soundfield at a particular time section and its
orientation will translate a lateralization effect eventually perceived by a
listener. These informations will be used to estimate an IACC associated to
a particular time segment. is explained along with the description of a method proposed by
Nakajima et al.[15] for the estimation of the IACC and
an alternative simple method which relates
is explained along with the description of a method proposed by
Nakajima et al.[15] for the estimation of the IACC and
an alternative simple method which relates 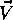 with possible IACC values for given temporal sections of the ETC.
with possible IACC values for given temporal sections of the ETC.
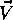 of components (
of components ( 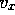 ,
, 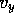 ,
, 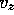 ) as viewed from each
receivers coordinate system is then constructed, where
) as viewed from each
receivers coordinate system is then constructed, where 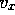 corresponds to
the receiver pointing direction,
corresponds to
the receiver pointing direction, 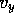 to the lateral direction and
to the lateral direction and 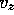 to the upward/downward direction. Once this vector is known, its three
components will provide the vertical and horizontal (
to the upward/downward direction. Once this vector is known, its three
components will provide the vertical and horizontal (  ,
,  ) angles of
incidence for a particular time section. The IACC can be estimated from
the vectors norm
) angles of
incidence for a particular time section. The IACC can be estimated from
the vectors norm 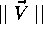 and from an equivalent angle
measured from the receivers median plane, a lateralization angle
and from an equivalent angle
measured from the receivers median plane, a lateralization angle
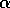 of the soundfield as seen from the receiver, where
of the soundfield as seen from the receiver, where
 . This approximation is
justified since we can consider the head as being almost symmetrical, so the
IACC is mainly determined from the reflection angle measured from the
median plane [15].
. This approximation is
justified since we can consider the head as being almost symmetrical, so the
IACC is mainly determined from the reflection angle measured from the
median plane [15].
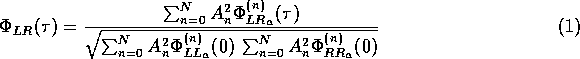
 is the time delay of sound signals between both ears, and ranges
from -1ms to +1ms to include the maximum interaural delay.
is the time delay of sound signals between both ears, and ranges
from -1ms to +1ms to include the maximum interaural delay. 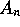 is the
pressure amplitude of the nth reflection relative to the direct
sound.
is the
pressure amplitude of the nth reflection relative to the direct
sound. 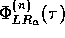 is the CCF of the signals for the
nth reflection and its associated lateralization angle
is the CCF of the signals for the
nth reflection and its associated lateralization angle 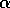 .
.
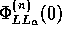 and
and  are
autocorrelation values ACF at
are
autocorrelation values ACF at  =0 (arrival time of the direct sound) of the
signals at the left and right ears, for the nth reflection and
associated lateralization angle
=0 (arrival time of the direct sound) of the
signals at the left and right ears, for the nth reflection and
associated lateralization angle 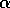 .
The interaural cross-correlation coefficient IACC corresponds to the maximum
absolute value of the function.
.
The interaural cross-correlation coefficient IACC corresponds to the maximum
absolute value of the function.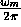 , are calculated by the following equation:
, are calculated by the following equation:
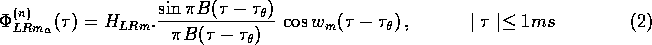
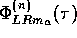 is the CCF per octave band ( m ) of
the signals for the nth reflection, B is the effective bandwidth of the
noise;
is the CCF per octave band ( m ) of
the signals for the nth reflection, B is the effective bandwidth of the
noise; 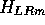 is the crosspower of mth bandpass filtered source signals
at both ears normalized by that of
is the crosspower of mth bandpass filtered source signals
at both ears normalized by that of 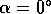 (frontal incidence).
The value of
(frontal incidence).
The value of 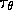 indicates the delay at the maximum of the
cross-correlation function, which depends on
indicates the delay at the maximum of the
cross-correlation function, which depends on 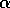 .
.
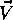 to possible
IACC values.
to possible
IACC values.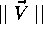 will equal unity. In an
ideally diffuse sound field, the cross-correlation between two omnidirectional
microphones is related to the ratio sin(kr)/kr, r being the distance
between both receivers. At low frequencies, the receivers will be closer to
each other relative to the wavelength, so high correlations are to be
expected. While
will equal unity. In an
ideally diffuse sound field, the cross-correlation between two omnidirectional
microphones is related to the ratio sin(kr)/kr, r being the distance
between both receivers. At low frequencies, the receivers will be closer to
each other relative to the wavelength, so high correlations are to be
expected. While 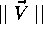 will reach a value very close to zero at
all frequencies, IACC will vary depending on the octave band.
will reach a value very close to zero at
all frequencies, IACC will vary depending on the octave band. )D up to a maximum established by a set of
free field measurements which will depend on the lateralization angle
)D up to a maximum established by a set of
free field measurements which will depend on the lateralization angle
 . So, each estimated IACC(
. So, each estimated IACC( ) per time segment from
simulations, IACC(
) per time segment from
simulations, IACC( ,t) will be a function of the following variables:
the free field IACC(
,t) will be a function of the following variables:
the free field IACC( ,
, ), the diffuse field
IACC(
), the diffuse field
IACC( )D and
)D and 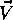 :
:
 ))
within the integration limits t1 and t2:
))
within the integration limits t1 and t2:
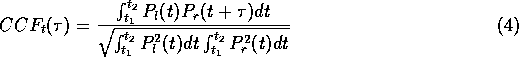
 the time shift, ranging from +1ms to -1ms to include the maximum
interaural delay.
the time shift, ranging from +1ms to -1ms to include the maximum
interaural delay.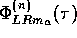 are periodical functions with several maxima (their separation depending on
frequency), reflections coming from different directions interfere with each
other and contribute to increase the measured inter-receiver variability, on
the other. Actually our method is closer to an approximation of the CCF by
their envelopes, i.e. where the estimation of the IACC from the mean
incident vector is equivalent to the estimation of IACC calculated from the superposition
of the envelopes of the
are periodical functions with several maxima (their separation depending on
frequency), reflections coming from different directions interfere with each
other and contribute to increase the measured inter-receiver variability, on
the other. Actually our method is closer to an approximation of the CCF by
their envelopes, i.e. where the estimation of the IACC from the mean
incident vector is equivalent to the estimation of IACC calculated from the superposition
of the envelopes of the 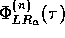 in equation 1.
in equation 1.
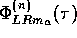 periodicity.
periodicity.]ms